TRIGONOMETRÍA DE EXAMEN ADMISIÓN RESUELTO PDF

¿Qué requieres saber para aprender, comprender y aplicar los conceptos, definiciones y teoremas de la Trigonometría?

Sería extenso recordarte todo lo que se supone has aprendido hasta ahora, pero en la medida que hayas desarrollado una cultura matemática se hará mas comprensible esta importante área de la ciencia, sin embargo, vale la pena puntualizar aspectos que deben merecer una permanente atención y evocación.

PREGUNTA 1 :

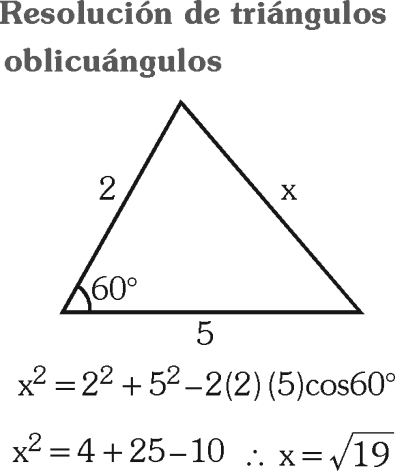
En un triángulo rectángulo, la tangente de uno de sus ángulos agudos es 8/15. Determina su cateto mayor si la hipotenusa es 17√2 .

A) 12√2

B) 10√2

C) 13√2

D) 8√2

E) 15√2

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 2 :

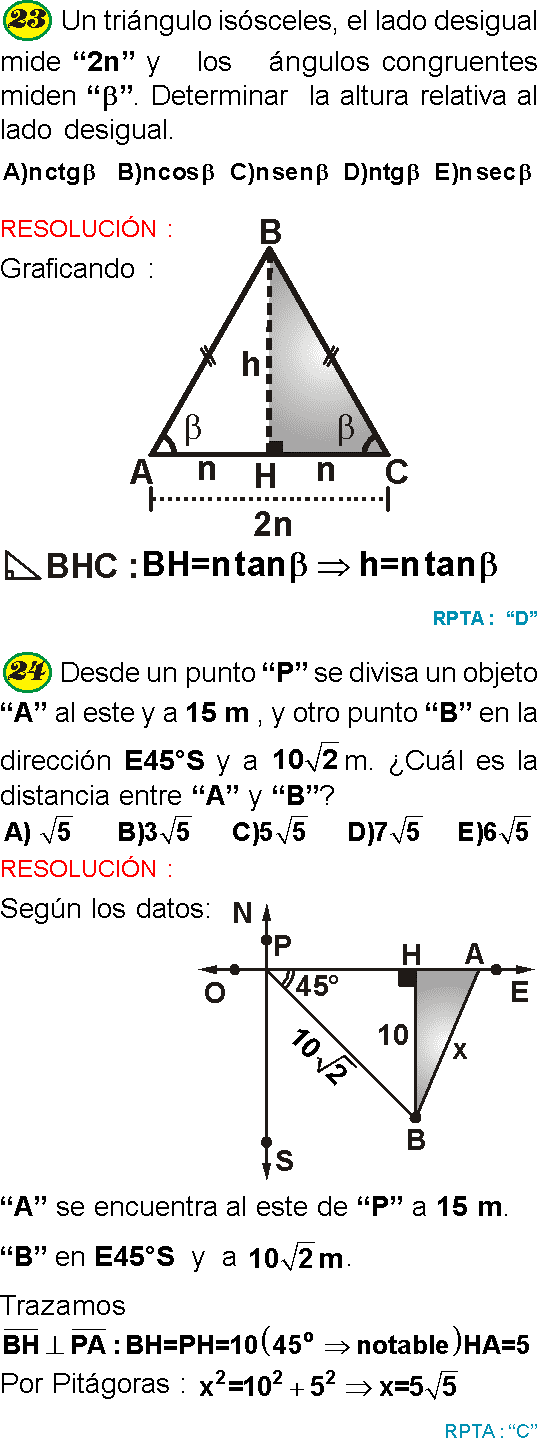
Un niño está volando una cometa. En determinado momento, la cuerda que sujeta la cometa mide 50 m, formando con el suelo un ángulo de 37º. Determine a qué altura se encuentra la cometa.

A) 40 m

B) 50 m

C) 20 m

D) 30 m

E) 40 m

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 3 :

Del gráfico, calcula tgθ si cos37°=4/5

A) 1/3

B) 2/5

C) 1

D) 3/4

E) 2/3

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 4 :

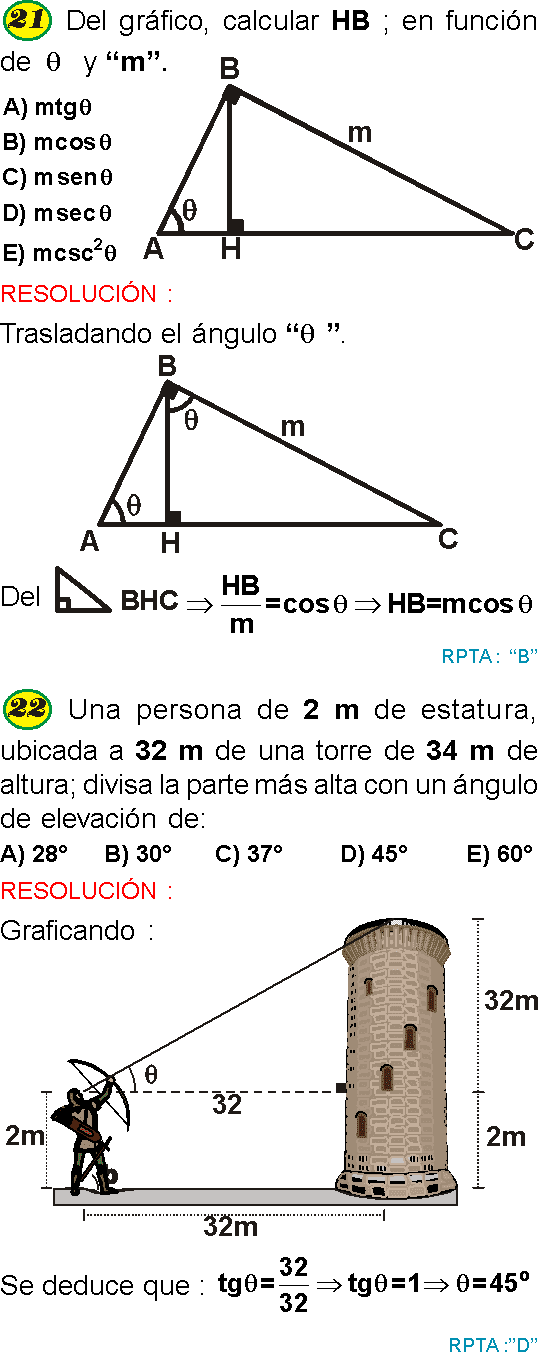
Del gráfico, determina “x”.

A) √11

B) √13

C) √17

D) √19

E) √14

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 5 :

En un triángulo dos de sus lados miden 3cm y 4cm y el ángulo comprendido entre ellos mide θ. si: Cosθ=–11/24 , calcular el perímetro del triángulo.

A) 9

B) 11

C) 14

D) 15

E) 13

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 6 :

Se tienen dos ángulos que sumados son 5𝛑/4 rad y su diferencia es 75°. Determina el suplemento del mayor de los ángulos en radianes.

A) 𝛑/12 rad

B) 𝛑/8 rad

C) 𝛑/4 rad

D) 𝛑/3 rad

E) 𝛑/6 rad

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 7 :

En el cuadro siguiente, unir mediante flechas.

A) IB, IIF, IIIC

B) IC, IID, IIIB

C) ID, IIA, IIIC

D) IB, IIC, IIID

E) IB, IID, IIIF

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 8 :

Calcula:

A) 1/11

B) 1/44

C) 19/44

D) 19/11

E) 5/8

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 9 :

Si: cosx ctgx = 3

determina cscx – senx.

A) 1

B) 2

C) 6

D) 4

E) 3

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 10 :

Si se cumple

ctgx +tgx + csc2x = 4

Determina :

A) 1/7

B) 7

C) 3

D) 2

E) 6

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 11 :

Determinar la relación entre el área de un sector circular, cuyo ángulo central es 2𝛑/5 radianes, y el área de un círculo, sabiendo que tienen el mismo radio.

A) 2/5

B) 1/5

C) 3/5

D) 5

E) 7/9

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 12 :

Del gráfico mostrado, hallar tgθ, si tgα= 5/8

A) 4/5

B) 5/2

C) 3/2

D) 5/3

E) 5/4

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 13 :

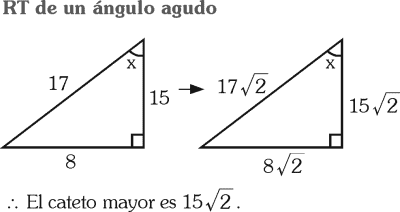
Una persona parte desde A hacia B con rumbo S60º0, luego se dirige hacia C con rumbo S75ºE, hasta ubicarse al sur de A. Si la distancia entre A y C es 10 m; halle aproximadamente la distancia entre B y C.

A) 10 m

B) 20 m

C) 15 m

D) 18 m

E) 5√6 m

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 14 :

Calcular:

2(a – b)senπ/2 +3(a – b)cosπ – (b – a)cscπ/2

A) a–b

B) 2(a+b)

C) 4(a–b)

D) 0

E) ab

RESOLUCIÓN :

R.T. de un ángulo de cualquier magnitud

=2(a – b)(1) +3(a – b)(–1) – (b – a)(1)

=2a – 2b – 3a+3b – b+a

Rpta. : "D"

PREGUNTA 15 :

Sabiendo que 0 ≤ 2θ ≤ π; además, senθ.cosθ= 1/4

Calcule

E = senθ + cosθ

A) 3/2

B) √(3/2)

C) √3/2

D) √2/2

E) 1

RESOLUCIÓN :

Identidades de una variable Auxiliares

0 ≤ 2θ ≤ π

⇒ 0 ≤ θ ≤ π/2

E²=(senθ + cosθ)²

⇒ E²= 1 + 2senθ.cosθ

⇒ E²= 1 + 2 × 1/4

→ E²= 3/2 ⇒ E=±√3/2

Como θ∈IC

∴ E =√(3/2)

Rpta. : "B"

PREGUNTA 16 :

A) 1

B) 2

C) 3

D) 5

E) 4

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 17 :

En el siguiente gráfico se sabe que x² =a+b√2

Calcule E=a − b.

A) 90

B) 97

C) 92

D) 93

E) 91

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 18 :

Si (2tgα+1)(tgα+2)cos²α=3

Calcule senαcosα.

A) 0,60

B) 0,30

C) 0,25

D) 0,20

E) 0,40

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 19 :

Siendo la identidad sen(x+60º) − cos(x+30º)=asenx+bcosx

Determine: a − b

A) 0

B) 8/9

C) 2

D) − 1

E) 1

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 20 :

Reduzca:

A) 1

B) 0

C) − 1

D) 2

E) 1/7

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 21 :

A) 1

B) – 1

C) 2

D) – 2

E) 0,6

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 22 :

Del gráfico, calcula cosθ.

A) √3

B) 2√7/7

C) √7

D) 7√5 /5

E) 2/7

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 23 :

Calcule el número de soluciones en el intervalo: [0 ; 2𝛑] de la siguiente ecuación:

Sen2x=Senx

A) 2

B) 3

C) 4

D) 5

E) 6

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 24 :

Calcule la suma de las dos primeras soluciones positivas de la ecuación.

2Sen2x+2(Senx+Cosx)=– 1

A) 𝛑/6

B) 𝛑/3

C) 5𝛑/6

D) 11𝛑/6

E) 𝛑/8

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 25 :

Del gráfico, determine el Senx

A)√6/6

B)√6/7

C)√6/4

D)√6/3

E)√6/5

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 26 :

A) 𝛑/6

B) 𝛑/3

C) 𝛑/4

D) 𝛑/12

E) 𝛑/2

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 27 :

A) 1/3

B) 1/4

C) 1/5

D) 1/2

E) 2/3

RESOLUCIÓN :

Rpta. : "D"

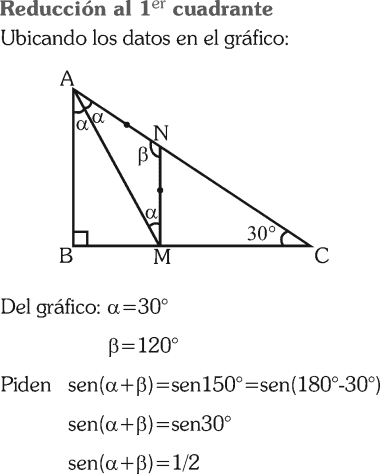
PREGUNTA 28 :

En el gráfico, AM es bisectriz del ángulo BAC; el ∠ACB=30°. Además α=∠NAM y β=∠MNA, siendo AN=NM; calcule sen(α+β)

A) 1/4

B) 3/2

C) 2/7

D) 3/5

E) 1/2

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 29 :

M= cos(θ)cos(2θ)cos(3θ)cos(4θ)csc(5θ)

Halla 64M, si θ= 15°

A) √6

B) 1

C) 8√6

D) 8

E) 6

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 30 :

Si 0 < x < 𝛑/2

calcula:

cos(x+𝛑)+cos(x+𝛑/2)+cos(x – 𝛑)+tg(x+𝛑)cos(x+𝛑)

A) senx – 2cosx

B) 3senx

C) 2senx

D) –2senx – 2cosx

E) 0

RESOLUCIÓN :

Rpta. : "D"

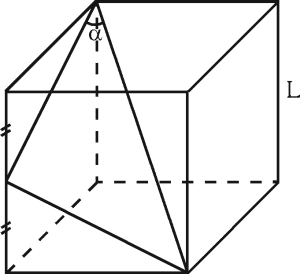
PREGUNTA 31 :

Del cubo mostrado, calcule :

(senα + cosα)÷(tanα + cotα ) ; el lado del cubo es L

A) 1

B) √30/5 [ √3+√2]

C) √6/5 [ √3+√2]

D) √30/25 [ √3+√2]

E)√6

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 32 :

En un triángulo ABC, de lados 3 y 4 unidades, el coseno del ángulo que forman dichos lados es – 11/24. Calcule el perímetro de dicho triángulo.

A) 10

B) 13

C) 15

D) 17

E) 14

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 33 :

Determinar la expresión correcta

I) Si x∈ ] 3𝛑/2 ; 2𝛑 [ ⇒ tgx es positiva.

II) Si x∈ ] 𝛑/2 ; 𝛑 [ ⇒ senx es creciente.

III) Si x∈ ] 𝛑 ; 3𝛑/2 [ ⇒ cosx es negativa.

A) Solo III

B) Solo I

C) Solo II

D) I y III

E) I ; II y III

RESOLUCIÓN :

Circunferencia trigonométrica

I) Si x∈ ] 3𝛑/2 ; 2𝛑 [ ⇒ tgx es negativa.

II) Si x∈ ] 𝛑/2 ; 𝛑 [ ⇒ es decreciente.

III) Si x∈ ] 𝛑 ; 3𝛑/2 [ ⇒ cosx es negativa.

Rpta. : "A"

PREGUNTA 34 :

Un observador de 1,7 m de estatura visualiza la parte alta de una antena colocada sobre un edificio, con ángulo de elevación de 37º; si se acerca 7 m hacia el edificio, el nuevo ángulo de elevación es 53º. Si la antena mide 1,5 m, determinar la altura del edificio.

A) 12,2 m

B) 13,2 m

C) 14,2 m

D) 15,2 m

E) 14,6 m

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 35 :

Sea la función, y=f(x)=tgx

Se sabe que:

Dom∈ [0;a] ∪ [b;π]

Ran ∈ [–√3 ;√3 ].

Hallar: a+b

A) π/4

B) π/3

C) π

D) 2π

E) π/5

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 36 :

El valor de Sen37º. Csc37º – tg45º. Ctg45º es

A) – 1

B) 0

C) 1

D) 2

E) 1/2

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 37 :

Sabiendo que

x + y=66°

x − y= 𝛑/30 rad

halle el mayor de los ángulos.

A) 𝛑/5 rad

B) 𝛑/4 rad

C) 𝛑/10 rad

D) 𝛑/9 rad

E) 𝛑/8 rad

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 38 :

Se tiene un globo inflado con helio atado con una cuerda al piso de un campo. Si un viento empuja al globo 30 m horizontalmente y si la cuerda que lo sostiene mide 50 m, calcule a qué altura del piso queda el globo.

A) 30

B) 40

C) 50

D) 45

E) 60

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 39 :

En un triángulo rectángulo que tiene un ángulo agudo “α” se cumple tgα=5senα/3.

Halle senα+cosα.

A) 6/5

B) 7/5

C) 1

D) 3

E) 1,3

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 40 :

Calcule el valor de

cos(2550°)+cos(−390°)

A) 1

B) √2

C) √3

D) 1/2 + √3/2

E) 2

RESOLUCIÓN :

cos(2550°)+cos(−390°)

=cos(360°.7+30°)+cos(−[360°+30°])

=cos(30°)+cos(30°)

= √3

Rpta. : "C"

PREGUNTA 41 :

Reduce :

A) senx

B) cosx

C) secx

D) cotx

E) tanx

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 42 :

Si: x – y= 𝛑/3

Calcular:

E=(cosx+cosy)²+(senx+seny)²

A) 1

B) 2

C) 3

D) 4

E) 5

RESOLUCIÓN :

Identidades trigonométricas de suma y diferencia de variables

Desarrollando los binomios al cuadrado :

E=cos²x+2cosx cosy+cos²y+sen²x+2senx seny+sen²y

Considerando que sen²y + cos²x=1 y agrupando , se ontendrá :

⇒ E=2+2(cosx cosy+senx seny)

⇒ E=2+2 cos(x – y)

⇒ E=2+2cos𝛑/3

⇒ E=2+2 (1/2)=3

Rpta. : "C"

PREGUNTA 43 :

Si x∈[40°; 290°], indica el número de soluciones en dicho intervalo de:

2√3 – 2√3cos²x=sen2x

A) 1

B) 5

C) 3

D) 4

E) 2

RESOLUCIÓN :

Ecuaciones trigonométricas

Factorizando 2√3 :

2√3(1 – cos²x)=2senxcosx

⇒ 2√3sen²x=2senxcosx

I) senx=0 → x=0°, 180°, 360°

II) √3senx=cosx → tanx=√3/3

∴ x=30°; 210°

⇒ x₁=180° ; x₂=210° dos soluciones

Rpta. : "E"

PREGUNTA 44 :

Si: sen(𝛑/2 + α ) – cos(α – 𝛑)= 1/2

Calcular : cosα+senα tgα

A) 1

B) 2

C) 3

D) 4

E) 5

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 45 :

A) 5

B) 7

C) 9

D) 11

E) 8

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 46 :

A) 3√3 ; 3 – √3

B) 6√2 ; 3 – √3

C) 3√2 ; 3 +√3

D) √3 ; 3 + √3

E) √6 ; 3 + √3

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 47 :

Si: θ=15º

M= cosθ. cos2θ . cos3θ . cos4θ . csc5θ

Calcular 64M²

A) 5

B) 16

C) 7

D) 8

E) 6

RESOLUCIÓN :

Propiedades de las razones trigonométricas de ángulos notables

Rpta. : "E"

PREGUNTA 48 :

Halle el rango de la función

F(x)=sen²x+2senx+π

A) [π; π+3]

B) [π−1; π+2]

C) [π−1; π+4]

D) [π+1; π+3]

E) [π−1; π+3]

RESOLUCIÓN :

Agregando y quitando 1 :

F(x)=sen²x+2senx+1+π−1

⇒ F(x)=(senx+1)²+π−1

⇒ −1 ≤ senx ≤ 1

⇒ 0 ≤ senx+1 ≤ 2

⇒ 0 ≤ (senx+1)² ≤ 4

⇒ π ≤ (senx+1)²+π ≤ 4+π

⇒ π −1 ≤ (senx+1)²+π−1 ≤ 4+π−1

⇒ π−1 ≤ F(x) ≤ π + 3

Rpta. : "E"

PREGUNTA 49 :

Si – 𝛑/2 ≤ x ≤ 0 , tal que

cosx=0

cos(x + z)=1/2

halle el menor valor de “z”.

A) 𝛑/4

B) 𝛑/3

C) 𝛑/8

D) 𝛑/12

E) 𝛑/6

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 50 :

A) 1

B) √3

C) √2

D) √3+1

E) √5

RESOLUCIÓN :

Rpta. : "B"

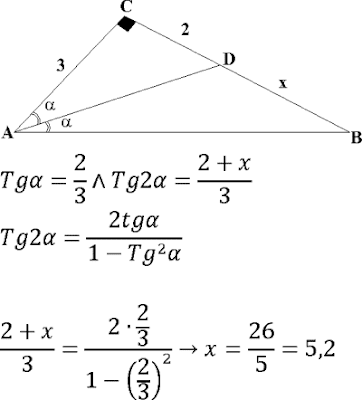
PREGUNTA 51:

En un triángulo rectángulo ABC (recto en C), la bisectriz del ángulo A interseca a su lado opuesto en D. Si DC=2, AC=3, halle el valor de BD.

A) 3,5

B) 4,0

C) 5,2

D) 6,0

E) 6,2

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 52:

Si “S” y “C” son los números de grados sexagesimales y centesimales respectivamente de un mismo ángulo, halle su medida en el sistema radial, sabiendo que:

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 53:

Carla se encuentra a una distancia de 40 m de un edificio y observa la parte más alta de él, con un ángulo cuya tangente es 7/10. Halle la distancia que debe alejarse Carla para que el nuevo ángulo de elevación tenga como tangente 1/3.

A) 44 m

B) 48 m

C) 50 m

D) 60 m

E) 40 m

RESOLUCIÓN :